
文/曹君辉 邵旭东
复核/黄政宇
导读:2001年9月11日,位于美国纽约曼哈顿的世贸大厦受到被劫持的飞机撞击,造成灾难性后果。沉痛的教训不仅促使全球安检系统升级,也迫使土木工程师们对结构的抗冲击性能予以空前的关注。通过往期分享的内容我们知道,超高性能混凝土(UHPC)基体致密且富含钢纤维,不仅具有较高的抗压强度和抗拉强度,还表现出优异的变形能力。混凝土的抗冲击性能与其变形能力密切相关,因而UHPC同样具有突出的抗冲击性能。本期将与各位分享UHPC抗冲击性能的研究成果,分为上、下两期,上期主要介绍UHPC在抗压、抗拉、抗弯拉等基本受力模式下的冲击性能,下期将主要介绍UHPC的抗冲击试验装置与方法,并探讨UHPC的抗冲击设计方法。
一、概述
土木工程结构在运营中同时承受静力和动力荷载作用。区分静、动力荷载的基本原则是:荷载大小或方向随时间变化的速率,当荷载变化极为缓慢时可视为静力荷载,反之则应划分为动力荷载(图1)。对于桥梁结构,常见的动力荷载主要包括车辆荷载、人群荷载、风荷载等,也有可能出现地震荷载,甚至可能遭受车辆撞击,船舶、冰块或其他漂浮物撞击、爆炸等强动力荷载。冲击荷载属于高应变率的动力荷载,在材料或结构上的作用时间一般小于自振周期1/3~1/2。
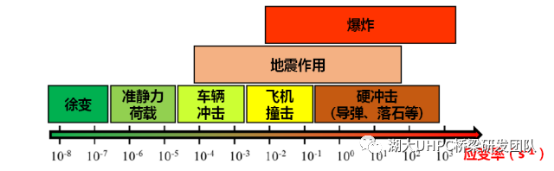
图1. 土木工程结构中的率相关荷载
在介绍UHPC的冲击性能之前,首先了解一下普通混凝土的动力性能。大量研究表明,混凝土的力学性能指标基本都是与荷载(或应变)率相关的,且一般规律为:应变率越高,混凝土的抗压强度、极限应变和断裂能等指标值也越高。
动力增长系数(DIF,Dynamic Increase Factor)是刻画混凝土动力性能的重要指标,其定义为混凝土的动力强度(fd)与静力强度(fs)之比,如式(1)所示。普通混凝土抗压、抗拉强度DIF随应变率的变化规律如图2所示。不难看出,混凝土的强度随着应变率的增加而增加,且抗拉强度的增加幅度更为明显。

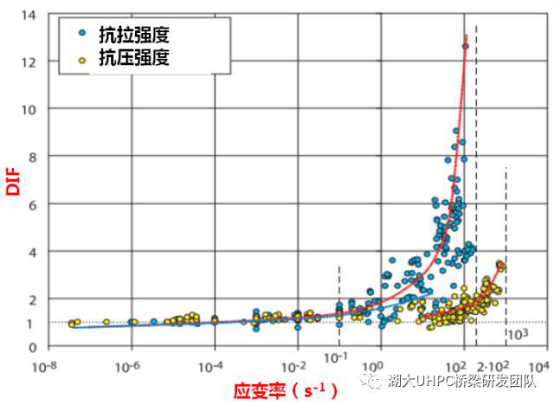
图2. 普通混凝土DIF随应变率的变化规律
为什么混凝土在动力荷载下的强度会提高?研究表明,一方面,由于混凝土内部存在孔隙,在高应变率下,空隙水压力迅速增加,协助混凝土骨架抵抗变形,从而提高了材料的强度。另一方面,在静力荷载下,裂缝一般沿着骨料-水泥基体间的薄弱面缓慢扩展,导致强度较低,而当应变率较高时,裂缝来不及寻找最薄弱的扩展路径,可能会穿过粗骨料,同样会提高材料的强度。
与普通混凝土相比,UHPC基于最大堆积密度原理配制,使得材料内部致密,同时,UHPC中掺入了大量的钢纤维。研究表明,这些措施能够进一步提高水泥基复合材料的抗冲击性能,原因是在冲击荷载下,高强水泥基体的破碎和钢纤维的拔出均能吸收大量冲击能量。同时,钢纤维的存在能够有效控制裂缝的发展,防止构件整体破坏,当配置钢筋时,这一效果更为突出(图3)。

图3. 密配筋混凝土CRC(一种UHPC)炮弹侵彻试验
上述组成特点使得UHPC的动力性能明显优于普通混凝土和常规的钢纤维混凝土,能够用于遭受强动力荷载的构件,甚至可用在军事结构和防护结构中。目前国内外学者已对UHPC的抗冲击性能进行了研究,涵盖了UHPC的抗压、抗拉、抗弯拉等多方面。下面对相关研究结果进行分享。
二、UHPC的抗压冲击性能
Rong Z.D.等基于分离式霍普金森压杆(SHPB,Split Hopkinson Pressure Bar)装置对高应变率下UHPC的轴压冲击性能进行了试验研究。UHPC中钢纤维的直径和长度分别为0.175mm和13mm,体积含量为Vf=0,3%,4%。通过试验,得到了各试件在动力荷载下的轴压应力-应变曲线(图4)
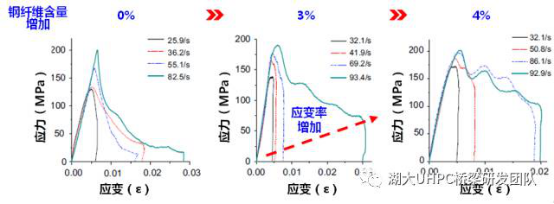
图4. 冲击荷载下UHPC轴压应力-应变曲线
由上图可知,1)所有应力-应变曲线的上升段基本上都呈直线,这一现象与UHPC在静力荷载下的轴压应力-应变曲线特征相似;2)对于给定纤维含量,应变率对UHPC的抗压性能影响显著,随着应变率的增加,试件的抗压强度、峰值应变及极限压应变均增加,同时,压缩韧性(即应力-应变曲线所包含的面积)也增加;3)钢纤维同样会影响UHPC的抗压动力性能,当纤维含量增加时,抗压强度和峰值应变相应增加,同时,曲线更加饱满,表明UHPC的抗压韧性得以提高。
UHPC在冲击荷载下的抗压破坏形态同样与应变率密切相关。如图5所示,当应变率较低时(25.9-50.8/s),试件基本完整,而当应变率较高时(82.5-93.4/s),不含钢纤维的UHPC试件已支离破碎,而含钢纤维的UHPC试件整体仍然保持完好,仅在试件侧面出现一些裂缝,且钢纤维含量越高,裂缝越少。因此,通过掺入钢纤维可以有效避免UHPC出现严重冲击破损现象。

图5. 冲击荷载下UHPC抗压破坏形态
田志敏等对UHPC的抗压冲击试验也表明(应变率为20-90/s),当荷载冲量较小时,UHPC的冲击损伤较小,而当荷载冲量增加到一定值(冲击破坏阈值)时,试件严重破坏,甚至被压碎至粉末状。根据试验结果,试件的静力抗压强度越高,其冲击破坏阈值越大。
三、UHPC的抗拉冲击性能
对UHPC的抗拉冲击试验表明,随着应变率的增加,UHPC的极限抗拉强度及所吸收的能量相应增加(图6),且UHPC可维持应变硬化现象,伴随着多裂缝的出现与扩展。因此,总体而言,高应变率会提高UHPC的轴拉性能。
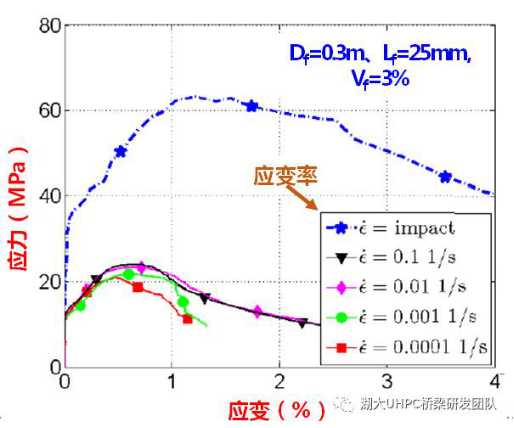
图6. UHPC轴拉动力应力-应变曲线
但是所掺入的钢纤维增加了UHPC轴拉冲击性能的复杂性。Tran T.N.等采用一种新型的应变能框架冲击装置测试了UHPC的轴拉冲击性能。共制作了两种尺寸的轴拉试件,截面尺寸分别为25×25mm2和25×50mm2。为探明钢纤维类型的影响,在UHPC试件中考虑了三种钢纤维,即扭曲纤维(T)、长直纤维(LS)、短直纤维(SS),三者的等效直径均为0.2mm,长度分别为20mm、19mm、13mm,钢纤维体积掺量均为1.5%。
试验表明,在静力荷载下,所有试件均具有应变硬化特性,极限抗拉强度为10-14 MPa。在应变率为5-24S-1的动力荷载作用下,轴拉试件仍表现出应变硬化特性,极限抗拉强度显著提高,达20-45 MPa。对轴拉力学参数的分析发现,在高应变率下,UHPC极限抗拉强度的DIF为1.2-3.3,极限拉应变的DIF为0.7-6.6,峰值韧性的DIF为0.6-7.6,而裂缝数量的DIF为0.6-1.6。整体而言,UHPC在高应变率下的抗拉性能指标要高于静力试验。需要说明的是,对于极限拉应变、峰值韧性和裂缝数量,一些DIF值小于1,这主要与动力试验技术和装置等因素有关,由于动力试验复杂,当试件-冲击装置间的局部接触不均匀时可能会出现这样的结果。
图7示意了钢纤维类型对UHPC轴拉力学指标在静、动荷载条件下的影响规律。在静力荷载下,UHPC轴抗拉性能指标(极限抗拉强度、极限拉应变、峰值韧性、裂缝数量)的规律均为:扭曲纤维T>长直纤维LS>短直纤维SS。而在高应变率下,长直纤维试件LS具有最高的极限抗拉强度、极限拉应变和峰值韧性。具体地,极限拉应变的高低顺序为:LS>T>SS,而极限拉应变和峰值韧性的高低顺序为LS≈SS>T,这些规律均与静力试验现象不一致;只有裂缝数量的高低顺序与静力试验结果一致,即T>LS>SS。
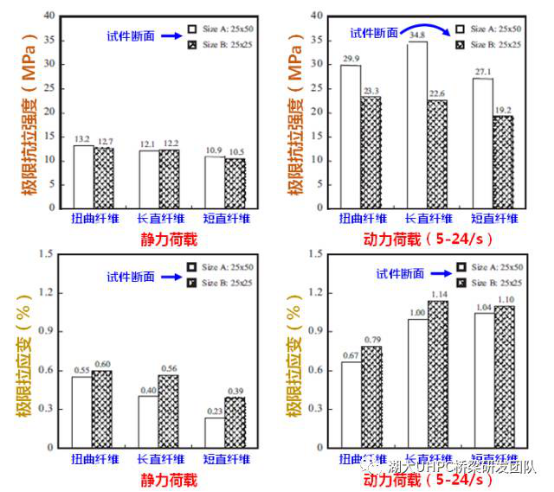
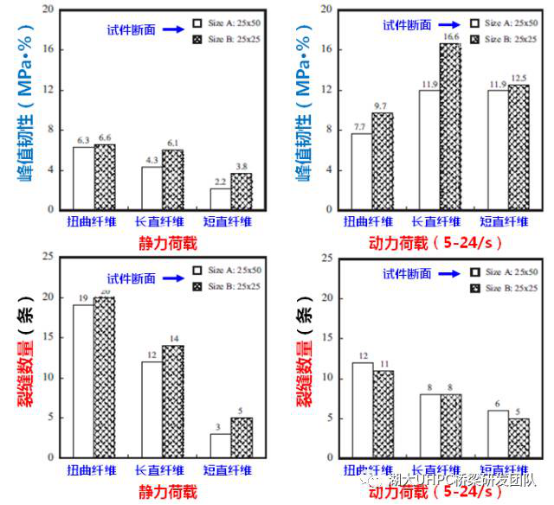
图7. 钢纤维对UHPC静、动力轴拉性能的影响
为何在静力荷载下,扭曲钢纤维UHPC的抗拉强度比长直钢纤维要高,而在高应变率下却相反?扭曲钢纤维与UHPC的界面粘结强度更高,自然提高了静力抗拉强度。而在高应变率下,钢纤维-UHPC界面间的粘结强度会进一步提高,且相比于长直钢纤维,变形钢纤维对应变率的敏感程度更高。受此影响,长直钢纤维UHPC试件中绝大多数(约97%)的钢纤维被拔出,而扭曲钢纤维UHPC试件中只有约79%的钢纤维被拔出,从而使得扭曲钢纤维UHPC在高应变率下的极限抗拉强度低于长直钢纤维UHPC。
同时,钢纤维-水泥基体粘结强度的提高使得纤维滑移降低,导致扭曲钢纤维UHPC试件中的裂缝宽度更窄。研究中通过高速摄像头记录了UHPC中的裂缝扩展过程,结果表明,扭曲纤维T、长直纤维LS、短直纤维SS试件中在峰值拉应力下的裂缝宽度分别为0.131mm、0.277mm、0.312mm(图8)。因此,高应变率下扭曲钢纤维UHPC的裂缝宽度较窄,从而降低了其极限拉应变。因此,为提高UHPC在动力荷载下的抗拉强度和极限拉应变,需要仔细考虑钢纤维-水泥基体间的粘结性能,避免钢纤维被拉断。
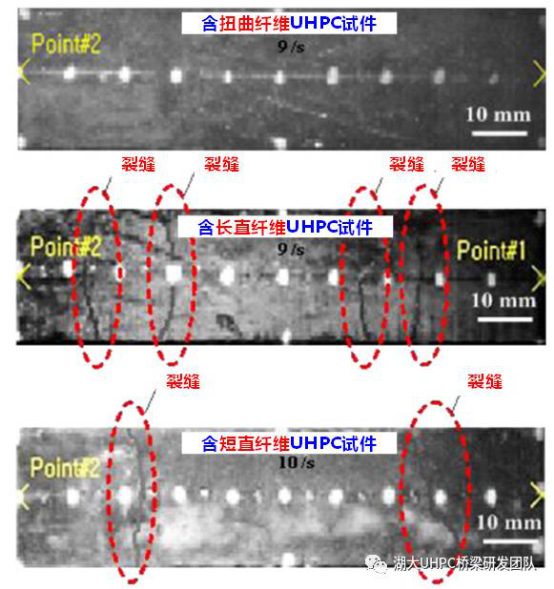
图8. 不同钢纤维UHPC在高应变率下的多缝开裂现象
由图7还可以看出,对于静力荷载,基于小尺寸试件得到的极限抗拉强度一般高于大尺寸试件,而对于动力荷载,基于大尺寸试件得到的极限抗拉强度更高。这一现象可解释为:大尺寸试件具有初始缺陷的概率越高,从而降低了静力抗拉性能。但在动力荷载下,受惯性力和应力波传播效应的影响,UHPC试件的动力行为更复杂。当试件尺寸减小时,试件的惯性力较小,从而降低了对试件所测得的应力历程,致使应力观测结果降低。然而目前的测试手段还难以准确捕捉惯性效应对抗拉强度的影响,因此,对于UHPC动力性能的尺寸效应问题还有待进一步探索。
UHPC中有时也会根据需求掺入合成纤维,为探明合成纤维对UHPC轴拉冲击性能的影响规律,Ravi R.等开展了试验研究。研究中制作了三种试件:1)轴拉试件,以测试UHPC在高应变率下的抗拉性能;2)PE单纤维拉出试件,以测试合成试纤维的拔出性能;3)带缺口的梁试件(不含纤维),以测试UHPC基体的断裂韧性。
基于轴拉试验,掌握了应变率对含PE纤维UHPC抗拉强度的影响规律,如图9所示。由该图可知,UHPC的初裂强度和极限抗拉强度均随加载率的增加而增加,当应变率由0.0001/s增加到10/s时,初裂强度增加了53%,极限抗拉强度增加了42%。但是极限拉应变和平均裂缝间距却持续降低,当应变率在0.0001/s-0.1/s之间时降幅较大,而当应变率超过0.1/s时,极限拉应变变化较小。
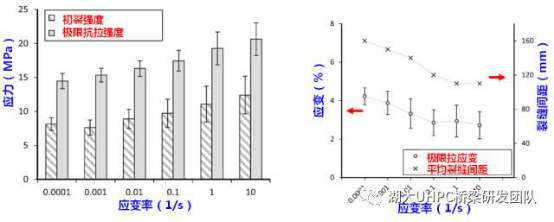
(a)抗拉强度 (b)极限拉应变和裂缝间距
图9. 应变率对含PE纤维UHPC轴拉性能的影响
上述规律应与水泥基体的断裂韧性、PE纤维特性以及纤维-水泥基体界面特性的动力效应有关。为探明这些因素的影响规律,分别对UHPC基体、PE纤维、PE-UHPC界面试件进行高应变率下的模型试验。结果发现,随着加载位移率的增加,UHPC基体(不含纤维)的抗拉断裂韧性稳步增长(图10a)。众所周知,纤维混凝土的初裂强度主要受基体强度影响,这就合理解释了含PE纤维UHPC初裂强度随应变率增加的现象。
同时,PE纤维的抗拉强度和弹性模量也会随着加载位移率的增加而增加。当加载位移率0.009mm/s增加到900mm/s时,PE纤维-基体界面粘结强度增加了14%(图10b),相比之下,纤维的抗拉强度和弹性模量增加更为明显,分别增加了21%和85%(图10c)。受这些特性的综合影响,UHPC在高应变率下的极限抗拉强度提高,同时,平均裂缝间距减小(图11),从而降低了试件的极限拉应变。
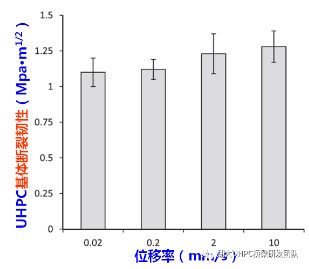
(a)UHPC基体断裂韧性
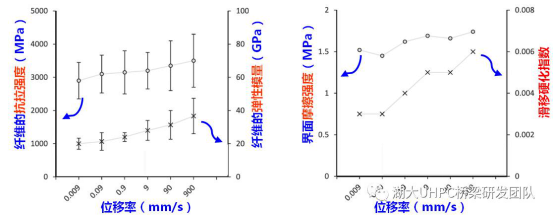
(b) 纤维抗拉强度与模量 (c)纤维-UHPC界面特性
图10. 加载率对UHPC基体、PE纤维、纤维-UHPC界面性能的影响

图11. 含PE纤维UHPC的多缝开裂现象
断裂能是刻画混凝土韧性的重要指标。国内外学者已经对混凝土材料进行了大量断裂能试验,但大多基于静力加载模式,而基于轴拉冲击试验开展的断裂能测试很少,对于UHPC尤甚。
Tran N. T.等探索了纤维类型和掺量对UHPC轴拉冲击断裂能的影响,应变率控制在5-92/s。整体而言,无论是在静力荷载还是动力荷载下,UHPC的断裂能均远高于常规混凝土材料(图12)。在高应变率下,UHPC的断裂能甚至高达80kJ/m2。
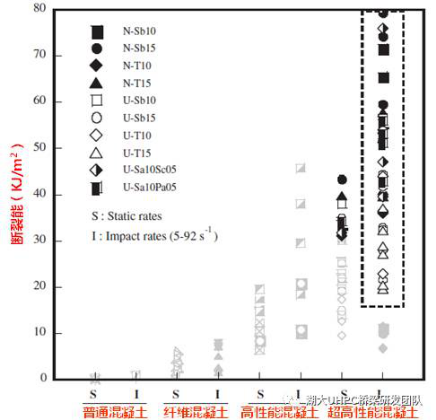
图12. 不同混凝土的断裂能
研究中定义特征断裂能为应力-应变曲线上升段所包围的面积,软化断裂能为下降段包含的面积。试验结果表明,特征断裂能对应变率十分敏感,在高应变率下DIF值约为1.2-10.2,表明应变率的提高能够增加UHPC的特征断裂能(图13)。
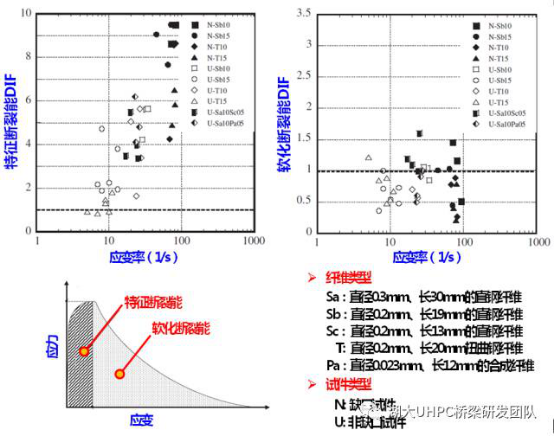
图13. 纤维对UHPC轴拉断裂能DIF的影响
相比之下,软化断裂能对应变率不太敏感,其DIF值在0.5-1.1之间,且具体值与纤维类型、含量等因素有关。由图13可知,含扭曲钢纤维UHPC试件的软化断裂能低于平直纤维。分析其原因仍然与纤维-水泥基体的界面粘结强度有关。由于扭曲纤维与UHPC的粘结强度更高,在高应变率下,相当一部分扭曲钢纤维被拉断(图14),而不是被拔出,这一现象降低了钢纤维跨裂缝间的桥接作用,从而降低了软化段的断裂能。而直纤维更多的是被拔出,进而可获得更高的断裂能。因此,根据这一研究结果,采用平直钢纤维对于优化高应变率下UHPC的轴拉断裂能更有利。

图14. 高应变率下扭曲钢纤维被拉断
四、UHPC的抗弯拉冲击性能
Bindiganavile V.等通过落重试验装置测试了几种混凝土材料(钢纤维混凝土、合成纤维混凝土、UHPC)的抗弯拉冲击性能。结果表明,当下落高度较小时,试件并未完全断裂,而当坠落高度较高时,试件断裂成两半(图15)。在接近破坏前,所有试件中的钢纤维均被拔出。
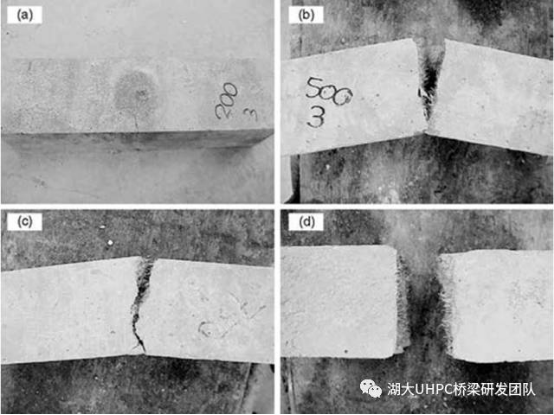
a)200mm;b)500mm;c)750mm;d)1000mm
图15. UHPC的抗弯拉破坏模式(下落高度)
与常规纤维混凝土相比,在冲击荷载下,UHPC能够耗散更多的能量。其主要原因是,UHPC具有高强的水泥基体和高含量的钢纤维,有效吸收了冲击能。图16对比了三种混凝土材料在不同落重高度下的弯曲韧性,结果表明,UHPC的弯曲韧性明显高于普通纤维混凝土FRC,约为后者的3-4倍。
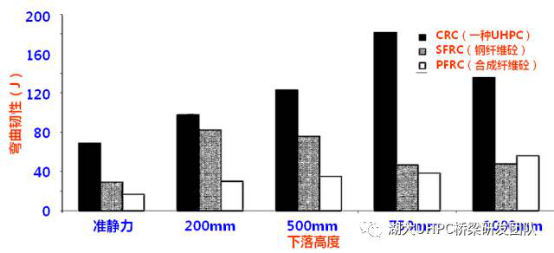
图16. 不同混凝土的冲击弯曲韧性
Habel K.等研究了UHPC板的抗弯冲击性能。试件为三点弯曲UHPC板。板件的尺寸为: 600mm(长)×145mm(宽)×50mm(高)。落锤重量为10.3kg和20.6kg,冲击瞬间速度约为4.2-4.3m/s,最大应变率约为2/s。试验发现,在第一次落锤中,跨中最大拉应变约为1%,第一次落锤后形成的残余应变为0.6%,但试件未出现大的裂缝。在随后的持续落锤中,板件受拉区出现了多缝开裂现象,在最后破坏阶段,试件跨中受拉区的钢纤维被拔出。
根据Millard S.G.等开展的抗弯拉冲击试验,当应变率小于1/s时,UHPC的抗弯拉强度DIF值接近于1,而当应变率大于1/s时,DIF值大致随着应变率(取对数)线性增加,斜率接近于1/3,如图17所示。
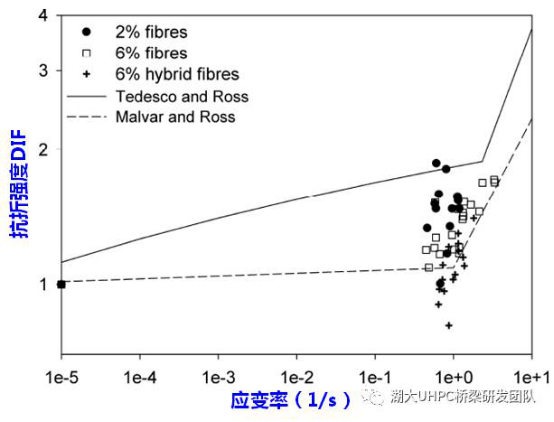
图17. 高应变率下UHPC抗弯拉强度DIF值
