周志敏

（广东冠生土木工程技术有限公司，广州，511400）

广东省交通运输厅科技项目，编号：科技-2013-02-001

摘要  针对我国沿海、内陆平原及山区广泛分布的软土上覆的硬壳层，简要介绍了硬壳层的成因、对其下软土的作用、以及硬壳层软基的承载力分析方法及沉降分析方法，为上覆硬壳层软基设计施工提供帮助。

关键词  软土  硬壳层  固结变形  性状

1.硬壳层下软基固结变形性状

在我国沿海和内陆平原地区分布着大量的软土地基，这些软土地基的表层由于水分蒸发，地下水位降低，荷载迁移，可溶盐及其它成份的沉淀等因素长期作用，形成了一层厚度不大但性质较好的土层，即所谓硬壳层。这种硬壳层面积广大，呈中等压缩性或低压缩性，胶结结构性强，与其下的软土层相比含水量和孔隙比较小，容重、变形模量和地基承载力较大。

1.1 硬壳层成因

1）地下水位影响

由于软粘土层出露于地表，开始蒸发失水，土层中地下水位下降，地下水在毛细力作用下向着地表面流动并蒸发。地下水位降低后，土体的有效应力增加，产生土体固结，使孔隙比减少。

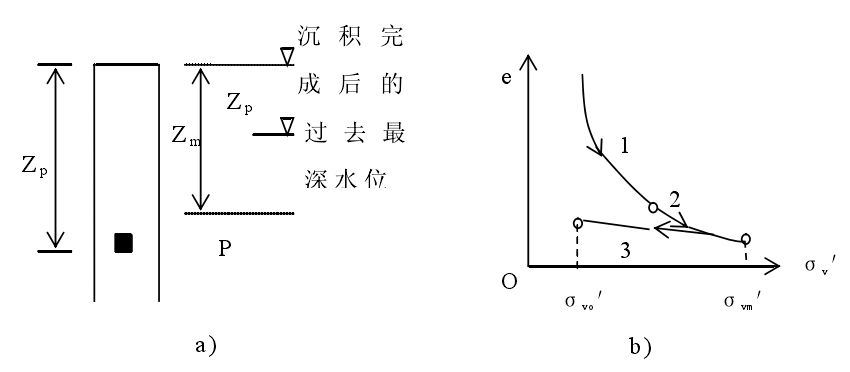
图2.1.1  地下水位变化对硬壳层的影响

2）化学风化

化学风化既能在水下也能在地面上发生，不过，一旦软粘土沉积表面上升到水面以上，风化作用立即加剧。土层顶部的风化由含有溶氧的雨水渗透所引起, 因此风化的深度由渗透深度和孔隙水的含氧量所决定。有两种基本的、决定风化结果的变化过程，即：（1）矿物的分解，（2）离子交换。控制这两个变化过程的方向和速率的环境因素是酸度值（PH值），氧化还原电势（Eh）和温度。

3）淋滤作用

淋滤是从土层剖面中排除易溶物质例如可溶盐的过程。这种过程可以在水力梯度下发生，也可以通过扩散产生。淋滤主要靠雨水引起，随着雨水的不断下渗，靠近地表的土层含盐量较低，随深度递增有一定量的增加，直到基本不变。

淋滤可以减少液限，而塑限下降不多，因此塑性指数减少，因含水量变化不大，因此被淋滤粘土的原状土强度下降。对上部硬壳层来说，淋滤作用虽然使原状土强度减小，因相对其它作用来说相对较小，因此影响不大。

4）胶结作用

如前所述，风化产物可以生成胶结物质。胶结是一种成岩过程，它的产生取决于软粘土沉积期所存在的物质。胶结粘土含有由强联结结合在一起的颗粒，这种联结具有与非胶结粘土不同的特性，在非胶结粘土中占优势的是“有效摩擦力”和“有效粘聚力”所产生的联结。胶结作用甚至表现为很大的抗拉强度或表现为很大的粘聚力。胶结作用增加了粘土结构的强度，并表现为较高的原状土强度和临界压力的增加。

1.2 硬壳层特殊作用

上覆硬壳层软土地基与一般的均质地基作用机理有很大的不同，主要表现在硬壳层的几个特殊作用，它们分别为壳体效应、封闭作用、滞后作用和反压护道作用等。

1.2.1 壳体效应

具有硬壳层的软土地基在荷载作用下，硬壳层与其下的软土层形成一整体的承力系统，软土层的工程特性与硬壳层有密切的关系。硬壳层本身具有相对较大的密实度，而且有一定的刚度，因此它可以分担荷载产生的一部分剪力，即在一定的荷载剪力作用下不产生剪切变形或变形极小，这就使得硬壳层与下卧软弱层间的荷载传递方式有了一定的变化，此时的硬壳层已具有了类似于板体的作用，这种作用可称为硬壳层的“壳体效应”又称为扩散作用。壳体效应可使外荷传到较大的下卧软土中，使其下卧软土层的附加应力低于按传统扩散方法计算出来的附加应力，且分布更加均匀，分布的范围更大。硬壳层的厚度愈大，相对刚度愈大，这种扩散作用越大。

1.2.2 封闭作用

软土中有大量自由水存在，而这种自由水在其连通的孔隙中是能够传递静水压力的。当软土层上具有硬壳层时, 硬壳层与软土层形成了较为鲜明的强度差和刚度差。硬壳层相对其下的软土既是一种柔性的却又类似板体的结构，它不仅能够将其下部承受的荷载传递到较大的面积上去，起到应力扩散的作用，同时对下卧淤泥土的变形具有较强的封闭作用。

1.2.3 路基沉降滞后作用

关于硬壳层作用的另一看法是硬壳层对沉降的滞后作用，它延缓了沉降速率，对沉降不利。假如填土荷载较大，而硬壳层又较薄，形成的沉降盆几乎完全破坏了硬壳层的支撑力，这时滞后效应将会明显；相反，硬壳层较厚，荷载低，支撑作用将会是主要的。实际上，大多数情况下沉降盆对硬壳层的破坏是微小的，所以滞后效应不明显。

1.2.4 反压护道作用

当硬壳层在荷载作用下失去板体作用后，如果路堤中心土压力继续增大，基础随着地基的压缩变形而下沉。当基础刺入一定深度后，路基基脚周围硬壳层土体发生垂直剪切破坏。在周围硬壳层下软土体的类帕斯卡效应下，路堤坡脚外侧的土压力便会从比较平稳变为逐渐增大，说明由于软土层的压缩产生的侧向变形对其上硬壳层产生了向上的作用力。路基下部硬壳层相当于设了高度等于下沉量的反压护道。在路堤不发生破坏的前提下，下沉量愈大，这种反压作用愈明显。

2  硬壳层软土地基极限承载力分析

含上覆硬壳层的软土地基本质上是上硬下软的双层地基，因此对该类型地基的研究类属于双层地基的研究。对于含上覆硬壳层的软土地基地基承载力的研究，国内外不少学者以均质地基承载力研究为基础，针对各自遇到的由不同类型土组成的双层地基进行了一系列深入探讨。

2.1 非均质介质地基极限承载力的几种理论计算方法

1）扩散角法

由太沙基（Terzaghi）和派克(Peck)提出的扩散角法计算非均质介质地基的基础极限承载力。该理论假定上部基底压力沿较硬土层向下线性扩散，直至下部软弱土层。如图 2.3.1 在两土层交界表面有一个长度宽度都变大的等效基础，在这个基础上的极限承载力即可等效为作用在下部较软土层基础的整体极限承载力承载力。可由式（2.5）进行计算。

                （2.5）

                 （2.6）

式中：

D — 基础的埋置深度；

H —上部土层的厚度；

qb — 下卧土层的极限承载力；

B — 基础的宽度；

Nc、Nq — 承载力系数；

γ1 — 上覆土体的容重。

图2.3.1  扩散角法计算简图

2）汉森加权平均法

当各土层的强度相差不是太大时，汉森建议采用按土厚度加权平均的方法计算整个地基的抗剪强度指标。若基层宽度为 B，则在滑动面最大切割深度 Zmax范围内的各土层指标均需参与加权平均计算。然后，用加权平均的抗剪强度指标计算地基极限承载力，持力层越薄，软弱下卧层所占的比重越大，加权平均抗剪强度指标下降越多，则整个地基的承载力越低。

根据汉森的建议，滑动面最大切割深度 Zmax由下式计算：

                       （2.7）

式中： B — 基础宽度（m）；

       λ — 系数，根据持力层的内摩擦角，由表2.1 查得。

表2.1   λ值表

然后取有效深度范围内不同土层的厚度或面积的加权平均强度而直接用均质土的汉森公式计算极限承载力容重和强度指标的计算如式（2.8）

                          （2.8）

式中：γi、ϕi、ci — 分别为第 i 层土的容重、内摩擦角和凝聚力；

              h — 第 i 层土的厚度。

计算示意图如图2.3.2。

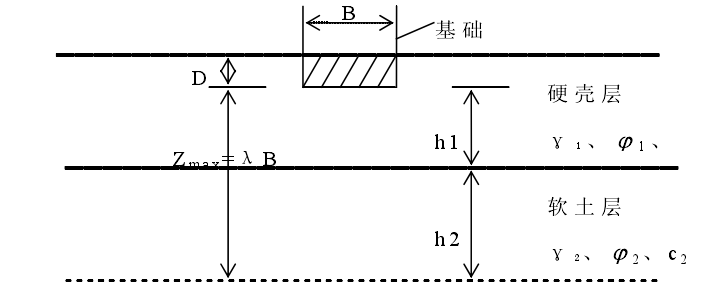
图2.3.2  汉森加权平均法示意图

因而成层土极限承载力可由式（2.9）所示公式进行计算。

         （2.9）

式中：sc、sq、sγ — 基础形状修正系数:

  ic、iq、iγ — 荷载倾斜修正系数；

  dc、dq、dγ — 基础埋深修正系数；

  gc、gq、gγ — 地面倾斜修正系数；

  bc、bq、bγ — 基底倾斜修正系数；

  Nc、Nq、Nγ — 承载力分项系数。

汉森的加权平均法，实际上就是把层状地基简化成以土的平均指标来表示的均质地基的一种近似方法。因此，当各土层的强度指标相差悬殊时，加权平均法不宜采用。

3） 迈耶霍夫和汉纳的冲剪破坏理论

迈耶霍夫和汉纳的冲剪破坏理论主要解决由两层土体（硬土层有下卧软土层）组成的地基的极限承载力问题，它假设地基基础中软弱土层上部的较硬土层发生剪切破坏，并假定剪切破坏面为竖直向下，如图2.3.3所示，地基底面与土层分界面之间的土体垂直地贯入软土层下卧软土发生弹塑性破坏，中间柱状土体受到两侧的被动土压力 Pp、 基础上部压力Q及下部软土层的反力qb，由极限平衡方程即可求得基础极限承载力。基础的承载力将由上下两土层联合组成，即：

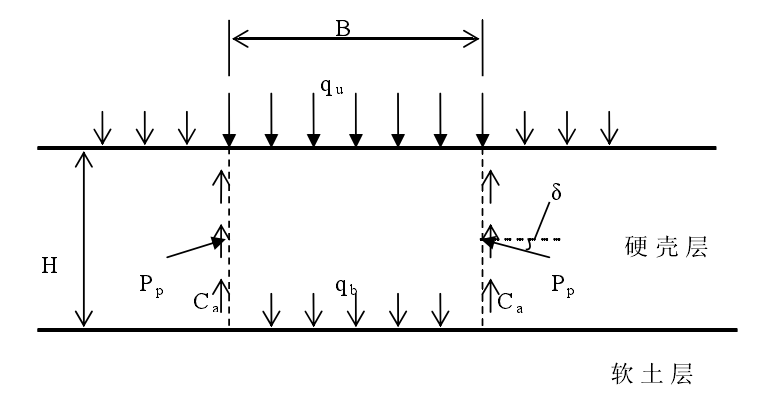
图2.3.3  迈耶霍夫、汉森理论计算示意图

            （2.10）

式中：qb —下卧土层的极限承载力；

  γ1 —上层土的容重；

  Pp  —上层剪切破坏面上的被动土压力；

  Ca — 破坏面上的附着力；

  δ — 被动土压力作用线与水平面的倾角。

下卧土层的极限承载力可由式（2.11）确定即：

               （2.11）

式中：Nc、Nq、Nγ — 承载力系数；

              γ2 — 下层土的容重；

              c2 — 下卧软土层的粘聚力；

              H — 硬壳层厚度。

3  硬壳层软土地基沉降估算

含硬壳层软土地基沉降可分为两部分，一部分是硬壳层在路基及车辆荷载作用下的压缩变形，另一部分是下伏软基的固结变形。

3.1 硬壳层变形估算

填筑土、沉积砂层、粘性土等承载力高和自身压缩模量大的硬壳层地基，已完成大部分固结变形，在一定范围新增路基荷载作用下硬壳层的土层在路基荷载作用下会产生变形，但杂填土或砂土等土体变形完成较快，一般在路基填筑完工后便可完成大部分变形，工后沉降量较小。因此，硬壳层的压缩变形近似按弹性变形估算。硬壳层压缩变形S1，即：

                        （2.1.2）

式中：σ1 —路堤硬壳层顶部压力；

  E1 —硬壳层弹性模量；

  H1  —硬壳层厚度；

  S1 — 硬壳层压缩变形。

  3.2 软基变形估算

根据软土的固结变形规律，采用分层总和法估算软基最终沉降量。分层总和法计算地基沉降是目前沉降计算中最普遍的方法。它在假定地基材料是弹性的、应力分布符合布西奈斯克解的同时，又假设地基材料是弹塑性的，其变形特性符合侧限一维压缩情况。用分层总和法计算最终沉降变形时一般取基底中心点下地基附加应力来计算各分层土的竖向压缩量，认为基础的平均沉降量 s 为各分层竖向压缩量Δsi之和。即得到下面的公式：

    （2.1.3）

式中：ΔPi — 第i层土体孔隙比e1i由变化到 e2i得到的基底附加应力增量；

        p0 — 基底附加压力；

       Esi — 基底第i层土的压缩模量；

        zi — 基底以下第i层至基底的距离；

        αi — 基底面第i层底面范围内的平均附加应力系数。