
文/ 曹君辉 邵旭东
复核/ 黄政宇
引言:在弯拉荷载作用下,UHPC表现出良好的抗疲劳性能,主要原因为:1)UHPC中无粗骨料,材料内部的应力集中显著降低;2)UHPC中掺有钢纤维,均匀分布的纤维能够有效阻止疲劳裂缝的增长与贯通。3)钢纤维与水泥基体间有较强的粘结强度,可进一步改善抗疲劳性能。本期与大家分享UHPC抗弯拉疲劳性能的相关研究,具体包含疲劳破坏特征、疲劳强度、变形规律、剩余强度等方面的内容。
一、UHPC的弯拉疲劳破坏模式与特征
曹霞等采用尺寸为35×35×244mm的试件,进行了UHPC的弯拉疲劳试验。试验中根据最大应力水平Smax(最大疲劳荷载引起的弯拉应力与静力弯拉强度之比)将试件分为四组,即Smax=0.75、0.8、0.85、0.9,共45个试件。
根据试验结果,试件的疲劳裂缝发展可分为以下三个阶段(图1):1)裂缝潜伏阶段,试件底端开始出现微小裂缝,但随着荷载循环次数的增加,试件表面未出现其他裂缝,该阶段约占总疲劳寿命的15%;2)裂缝稳定扩展阶段,随着循环次数继续增加,裂缝开始扩展增长,随着荷载变化,裂缝不断开合,疲劳裂缝逐渐扩展,该阶段占总疲劳寿命的75%左右;3)失稳破坏阶段,当循环次数超过总疲劳寿命的90%后,主裂缝迅速扩展,试件发生疲劳破坏,丧失承载力。

图1. UHPC弯拉疲劳破坏过程照片
试验中还观察到,当发生疲劳破坏时,试件裂缝处的温度比其他部位要高,说明裂缝在疲劳荷载作用下反复摩擦、挤压,伴随着热量的释放,这一现象在疲劳应力水平较低时尤为突出。
UHPC试件破坏时都伴随着UHPC基体的断裂和钢纤维的拔出。Al-Azzawi B.S.等的研究表明,在相同荷载条件下,当试件的疲劳寿命较短时,疲劳断裂面上的钢纤维分布不均匀,存在明显的低纤维含量区甚至是无纤维区(图2a),而当试件的疲劳寿命较长时,断裂面上的钢纤维分布较为均匀(图2b)。

(a)低疲劳寿命试件:纤维分布不均匀

(b)高疲劳寿命试件:纤维分布较均匀
图2.不同疲劳寿命UHPC试件中的纤维分布情况
Farhat F.A.等对疲劳破坏后的试件进行了疲劳断口分析,得到了疲劳断口中的钢纤维分布密度(图3),进一步证实了UHPC试件弯拉疲劳寿命与钢纤维分布的关联性:高疲劳寿命试件中的钢纤维分布一般较为均匀。
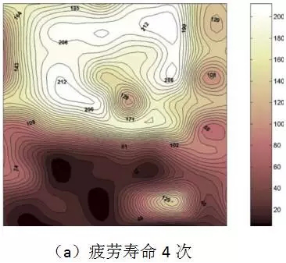
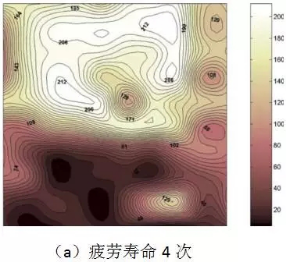
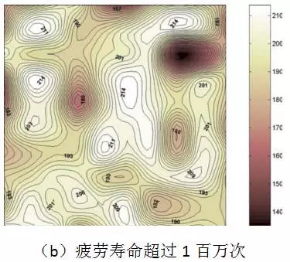
图3. UHPC试件疲劳断口中的钢纤维分布密度云图(单位:根/cm2,断面尺寸:100×100mm)
Graybeal B.A.等对预加载至开裂的UHPC试件进行了弯拉疲劳试验,结果表明,随着疲劳荷载循环次数的增加,初始裂缝逐渐增大,一些位于试件底部的钢纤维被拔出,而另一些钢纤维发生疲劳断裂,可听到钢纤维拔断的声音,图4a示意了原始钢纤维端面的微观形貌,图4b示意了疲劳断裂后的钢纤维端面形貌。这一现象说明,当UHPC基体开裂后,受应力重分布影响,钢纤维中的拉应力较高,可能出现钢纤维自身疲劳断裂现象。


图4. 钢纤维端面扫描电镜照片
二、UHPC的弯拉疲劳强度和S-N曲线
Parant E.等采用尺寸为40×200×600mm的试件,对UHPC进行了四点弯曲疲劳试验。这种UHPC中的钢纤维掺量高达11%,弯拉强度可达61.7 MPa。疲劳试验中控制最大应力水平Smax=0.7-1.03,Smax为疲劳荷载引起的最大弯拉应力与UHPC静力弯拉强度特征值(已考虑纤维取向系数)之比。
图5示意了主要试验结果。不难看出,当Smax不超过0.65时,所有试件的疲劳寿命均超过200万次。因此,这种UHPC的抗弯拉疲劳极限约为 Smax=0.65。
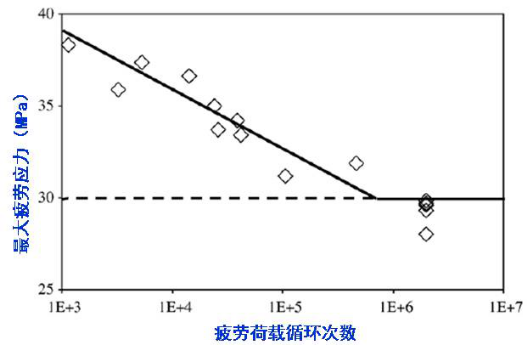
图5. 最大疲劳应力-荷载循环次数关系
在此基础上,作者还分析了应变-疲劳荷载循环次数关系,并通过拟合建立了计算方程,如图6所示。分析表明,UHPC试件的弯拉应变存在一个限值(约为1270-1440με),当疲劳应变不超过该限值时,试件在200万次循环内不会破坏,而当应变超过该限值时,试件的疲劳寿命大致与应变线性相关。

图6. 初始弯拉应变-疲劳荷载循环次数关系
Al-Azzawi B.S.等采用尺寸为35×100×340 mm的试件,对UHPC进行了弯拉疲劳试验。UHPC中所掺入的钢纤维直径为0.55mm,长度为30mm,体积含量为2.5%。试验中按最大应力水平将试件分为三组,即Smax=0.64、0.72、0.89,而最小应力水平保持恒定(Smin=0.1)。试验结果如图7所示,图中共包含两条曲线,一条为实测的S-N曲线,另一条为根据Goodman公式修正后,平均应力为零的S-N曲线。

图7. UHPC弯拉疲劳S-N曲线
由上图可知,平均弯拉应力(Smax+Smin)/2对UHPC抗弯拉疲劳强度的影响显著。相较于弯拉应力为零的情形,当平均弯拉应力大于零时,UHPC的疲劳强度明显降低。进一步分析表明,纤维的分布对UHPC的抗弯拉疲劳性能有显著影响:当钢纤维均匀分布时,其疲劳极限可达Smax=0.8;当纤维分布不均匀时,疲劳极限仅为Smax=0.64。
基于Basquin准则,作者通过数据拟合建立了UHPC弯拉疲劳的S-N曲线方程,如式(1)所示:

式中,σ0为平均应力为零时的应力幅;Nf为疲劳寿命;σF为UHPC的静力弯拉强度,该研究中为σF=22.02 MPa。
公式(1)要求平均应力为零,当平均应力大于零时,UHPC的弯拉疲劳寿命会降低,因而在实际应用中需要对应力幅进行换算,换算依据为Goodman公式,如式(2)所示。

式中,∆σσm为考虑非零平均应力修正的应力幅;σ0为平均应力为零时的应力幅;|σm| 为平均应力的绝对值;σF为UHPC的静力弯拉强度。
Lin M.等采用尺寸为40×40×160mm的试件,研究了钢纤维对UHPC弯拉疲劳寿命的影响,试验中最大应力水平为Smax=0.85,最小应力水平为Smin=0.15。UHPC中钢纤维直径为0.18-0.2mm,长度为12mm,而纤维体积掺量考虑了四种情形,即Vf=0%、1%、2%、3%。
试验结果表明,试件的疲劳寿命较好地符合Weibull分布。通过数据拟合,建立了不同钢纤维掺量下,UHPC的疲劳寿命计算公式,如式(3)-(6)所示,其中p为存活率:

在混凝土材料中,疲劳极限是衡量其疲劳性能的一项重要指标。对于UHPC,由于材料组分、纤维种类和掺量、试件尺寸等方面的差异,不同学者通过试验得出的UHPC疲劳极限结果存在一定差异。表1归纳了相关文献中对UHPC弯拉疲劳极限的建议取值,以供参考:
表1. UHPC弯拉疲劳极限试验结果归纳

三、UHPC的弯拉疲劳变形规律
曹霞等在试验中记录了UHPC试件的弯拉应变发展规律,试验结果如图8 所示。图中分别给出了最大应变和残余应变随疲劳荷载循环次数的变化规律。
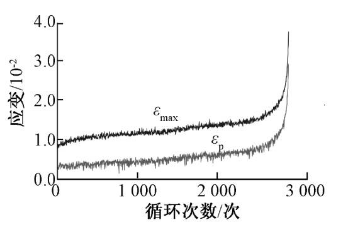
图8. 应变-荷载循环次数关系(Smax=0.9)
由图8可以看出,与裂缝发展的三阶段相似,UHPC 试件的应变也大体呈现三阶段变化模式:1)第一阶段,试件的纵向变形快速发展;2)第二阶段,变形随应力循环次数的增加而增长,此时UHPC的应变增率接近恒定;3)第三阶段,变形迅速增长,变形再次快速发展,试件历经短循环次数后破坏。试验同时表明,UHPC在第二阶段的应变增长率大致与最大应力水平Smax成正比。
Parant E.等对比了不同试件的挠度-循环次数曲线(图9)。从图9可以看出,试件的挠度发展也表现出三个典型阶段:1)第一阶段对应基体微裂缝开始开裂的阶段,挠度发展较快;2)第二阶段挠度增长缓慢,表明裂缝缓慢扩展;3)第三阶段,表明试件疲劳裂缝的失稳发展。需要说明的是,对于疲劳寿命较短的试件,挠度的三个发展阶段较为充分,而当试件经历200万次疲劳循环未破坏时,并未观察到第三个阶段。
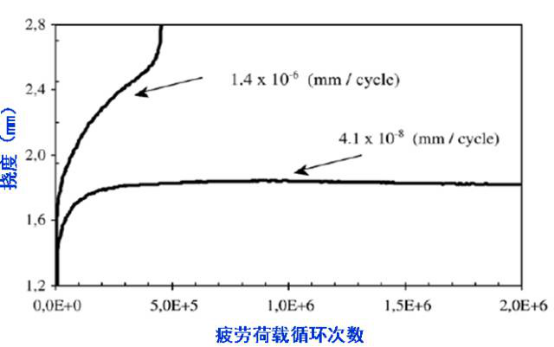
图9.挠度随荷载循环次数的变化规律
进一步分析发现,图9中两个试件的裂缝形态也存在差异。对于疲劳寿命较短的试件(1135次),试件受拉区出现了明显的集中裂缝(图10a),而对于疲劳寿命超过200万次的试件,裂缝分布较为均匀,且裂缝宽度较小,最大裂缝宽度不超过0.1mm(图10b),表现出良好的变形能力。
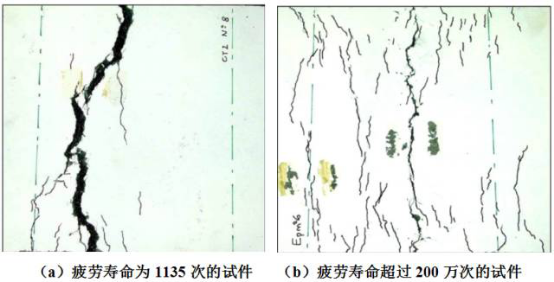
图10. 试件的两种疲劳裂缝分布形态
四、UHPC的弯拉疲劳剩余强度
Parant E.等在试验中对经历200万次疲劳循环而未破坏的试件进行了静力试验,得到了试件在疲劳试验后的应力-挠度曲线,并与未经历疲劳试验的试件进行了对比(图11)。

图11. 疲劳试验前后,UHPC试件弯拉应力-挠度曲线对比
可以看出,对于经历200万次疲劳荷载循环后的试件,其弯拉强度与未经历疲劳试验的试件十分接近。因此,在疲劳荷载作用下,UHPC的弯拉强度并无明显衰减,表明UHPC在弯拉荷载下表现出良好的抗疲劳性能。
